Homework 2

Chapter 19

6, 12, 15, 30, 36, 52

Q1

19-6. Calculate the minimum amount of work required to compress 5.00 moles5.00 \text{ moles} of an ideal gas isothermally at 300 K300 \text{ K} from a volume of 100 dm3100 \text{ dm}^3 to 40.0 dm340.0 \text{ dm}^3.

19-6. 计算在 300 K300 \text{ K} 下，将 5.00 摩尔5.00 \text{ 摩尔} 理想气体从 100 dm3100 \text{ dm}^3 等温压缩到 40.0 dm340.0 \text{ dm}^3 所需的最小功。

Q2

19-12. One mole of a monatomic ideal gas initially at a pressure of 2.00 bar2.00 \text{ bar} and a temperature of 273 K273 \text{ K} is taken to a final pressure of 4.00 bar4.00 \text{ bar} by the reversible path defined by P/V=constantP/V = \text{constant}. Calculate the values of ΔU\Delta U, ΔH\Delta H, qq, and ww for this process. Take CˉV\bar{C}_V to be equal to 12.5 J⋅mol−1⋅K−112.5 \text{ J} \cdot \text{mol}^{-1} \cdot \text{K}^{-1}.

19-12. 一摩尔单原子理想气体，初始压力为 2.00 bar2.00 \text{ bar}，温度为 273 K273 \text{ K}，沿着由 P/V=常数P/V = \text{常数} 定义的可逆路径，最终压力达到 4.00 bar4.00 \text{ bar}。计算该过程的 ΔU\Delta U、ΔH\Delta H、 qq 和 ww 的值。设 CˉV\bar{C}_V 等于 12.5 J⋅mol−1⋅K−112.5 \text{ J} \cdot \text{mol}^{-1} \cdot \text{K}^{-1}。

Q3

19-15. Show that

T2T1=(V1V2)R/CˉV\frac{T_2}{T_1} = \left(\frac{V_1}{V_2}\right)^{R/\bar{C}_V}

for a reversible adiabatic expansion of an ideal gas.

19-15. 证明对于理想气体的可逆绝热膨胀，有

T2T1=(V1V2)R/CˉV\frac{T_2}{T_1} = \left(\frac{V_1}{V_2}\right)^{R/\bar{C}_V}

Q4

19-30. Given that (∂U/∂V)T=0(\partial U/\partial V)_T = 0 for an ideal gas, prove that (∂H/∂V)T=0(\partial H/\partial V)_T = 0 for an ideal gas.

19-30. 已知对于理想气体 (∂U/∂V)T=0(\partial U/\partial V)_T = 0，证明对于理想气体 (∂H/∂V)T=0(\partial H/\partial V)_T = 0。

Q5

19-36. Given the following data, H2(g)+F2(g)→HF(g)ΔfH∘=−273.3 kJ⋅mol−1\text{H}_2\text{(g)} + \text{F}_2\text{(g)} \rightarrow \text{HF(g)} \quad \Delta_f H^\circ = -273.3 \text{ kJ} \cdot \text{mol}^{-1} H2(g)+12O2(g)→H2O(l)ΔfH∘=−285.8 kJ⋅mol−1\text{H}_2\text{(g)} + \frac{1}{2}\text{O}_2\text{(g)} \rightarrow \text{H}_2\text{O(l)} \quad \Delta_f H^\circ = -285.8 \text{ kJ} \cdot \text{mol}^{-1} calculate the value of ΔrH\Delta_r H for the reaction described by 2F2(g)+2H2O(l)→4HF(g)+O2(g)2 \text{F}_2\text{(g)} + 2 \text{H}_2\text{O(l)} \rightarrow 4 \text{HF(g)} + \text{O}_2\text{(g)}

19-36. 根据以下数据，

H2(g)+F2(g)→HF(g)ΔfH∘=−273.3 kJ⋅mol−1\text{H}_2\text{(g)} + \text{F}_2\text{(g)} \rightarrow \text{HF(g)} \quad \Delta_f H^\circ = -273.3 \text{ kJ} \cdot \text{mol}^{-1}

H2(g)+12O2(g)→H2O(l)ΔfH∘=−285.8 kJ⋅mol−1\text{H}_2\text{(g)} + \frac{1}{2}\text{O}_2\text{(g)} \rightarrow \text{H}_2\text{O(l)} \quad \Delta_f H^\circ = -285.8 \text{ kJ} \cdot \text{mol}^{-1}

计算反应 2F2(g)+2H2O(l)→4HF(g)+O2(g)2 \text{F}_2\text{(g)} + 2 \text{H}_2\text{O(l)} \rightarrow 4 \text{HF(g)} + \text{O}_2\text{(g)} 的 ΔrH\Delta_r H 值。

Q6

19-52. In this problem, we will discuss a famous experiment called the Joule-Thomson experiment. In the first half of the 19th century, Joule tried to measure the temperature change when a gas is expanded into a vacuum. The experimental setup was not sensitive enough, however, and he found that there was no temperature change, within the limits of his error. Soon afterward, Joule and Thomson devised a much more sensitive method for measuring the temperature change upon expansion. In their experiments (see Figure 19.11), a constant applied pressure P1P_1 causes a quantity of gas to flow slowly from one chamber to another through a porous plug of silk or cotton. If a volume, V1V_1, of gas is pushed through the porous plug, the work done on the gas is P1V1P_1 V_1. The pressure on the other side of the plug is maintained at P2P_2, so if a volume V2V_2 enters the right-side chamber, then the net work is given by

w=P1V1−P2V2w = P_1 V_1 - P_2 V_2

The apparatus is constructed so that the entire process is adiabatic, so q=0q = 0. Use the First Law of Thermodynamics to show that

U2+P2V2=U1+P1V1U_2 + P_2 V_2 = U_1 + P_1 V_1

or that ΔH=0\Delta H = 0 for a Joule-Thomson expansion. Starting with

dH=(∂H∂P)TdP+(∂H∂T)PdTdH = \left(\frac{\partial H}{\partial P}\right)_T dP + \left(\frac{\partial H}{\partial T}\right)_P dT

show that

(∂T∂P)H=−1CP(∂H∂P)T\left(\frac{\partial T}{\partial P}\right)_H = -\frac{1}{C_P} \left(\frac{\partial H}{\partial P}\right)_T

Interpret physically the derivative on the left side of this equation. This quantity is called the Joule-Thomson coefficient and is denoted by μJT\mu_{JT}. In Problem 19–54 you will show that it equals zero for an ideal gas. Nonzero values of (∂T/∂P)H(\partial T/\partial P)_H directly reflect intermolecular interactions. Most gases cool upon expansion [a positive value of (∂T/∂P)H(\partial T/\partial P)_H] and a Joule-Thomson expansion is used to liquefy gases.

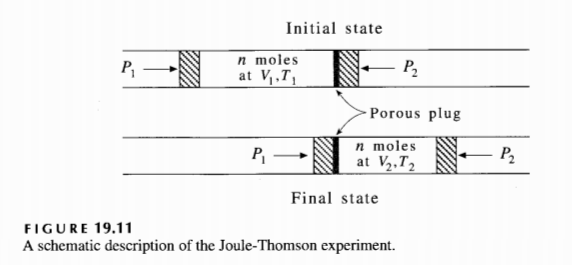
1757819011998

FIGURE 19.11

A schematic description of the Joule-Thomson experiment.

19-52. 在这个问题中，我们将讨论一个著名的实验，称为焦耳-汤姆孙实验。在19世纪上半叶，焦耳试图测量气体向真空中膨胀时的温度变化。然而，实验装置不够灵敏，他发现在他的误差范围内，没有温度变化。不久之后，焦耳和汤姆孙设计了一种更灵敏的方法来测量膨胀时的温度变化。在他们的实验中（见图19.11），一个恒定的施加压力 P1P_1 使一定量的气体通过丝绸或棉花制成的多孔塞从一个腔室缓慢流向另一个腔室。如果体积为 V1V_1 的气体被推过多孔塞，对气体所做的功为 P1V1P_1 V_1。塞子另一侧的压力保持在 P2P_2，因此如果体积为 V2V_2 的气体进入右侧腔室，那么净功由下式给出

w=P1V1−P2V2w = P_1 V_1 - P_2 V_2

该装置的构造使得整个过程是绝热的，因此 q=0q = 0。使用热力学第一定律证明

U2+P2V2=U1+P1V1U_2 + P_2 V_2 = U_1 + P_1 V_1

或者说，对于焦耳-汤姆孙膨胀，ΔH=0\Delta H = 0。从

dH=(∂H∂P)TdP+(∂H∂T)PdTdH = \left(\frac{\partial H}{\partial P}\right)_T dP + \left(\frac{\partial H}{\partial T}\right)_P dT

出发，证明

(∂T∂P)H=−1CP(∂H∂P)T\left(\frac{\partial T}{\partial P}\right)_H = -\frac{1}{C_P} \left(\frac{\partial H}{\partial P}\right)_T

请物理解释此方程左侧的导数。这个量被称为焦耳-汤姆孙系数，用 μJT\mu_{JT} 表示。在问题19–54中，你将证明对于理想气体，它等于零。(∂T/∂P)H(\partial T/\partial P)_H 的非零值直接反映了分子间的相互作用。大多数气体在膨胀时会冷却[即 (∂T/∂P)H(\partial T/\partial P)_H 为正值]，焦耳-汤姆孙膨胀被用于液化气体。

1757819011998

图 19.11

焦耳-汤姆孙实验的示意图。